之前我们讲了 线性分类器
深度学习修炼(一)线性分类器 | 权值理解、支撑向量机损失、梯度下降算法通俗理解_Qodi的博客-CSDN博客
又讲了基于线性分类器的全连接神经网络
深度学习修炼(二)全连接神经网络 | Softmax,交叉熵损失函数 优化AdaGrad,RMSProp等 对抗过拟合 全攻略_Qodi的博客-CSDN博客
但是 单纯的线性非线性操作有着比较大的局限性
一方面这种全连接网络参数量巨大,另一方面对于位置信息表现比较差。而今天的卷积神经网络非常重要,可以捕捉输入数据中的位置信息,这使得它在处理具有明显空间结构的数据时如图片表现优异。
1. 卷积基本操作
卷积操作可以将输入数据映射为输出数据,同时保留输入数据的空间结构信息。
假设我们有一个3x3的图像像素矩阵,如下所示:
1 | 1 2 3 |
我们希望对这个图像进行卷积操作。为了实现这个操作,我们需要定义一个卷积核(也称为过滤器)来滑动在图像上,从而产生一个新的输出图像。
卷积核
1 | 1 0 |
卷积操作的基本思想是在输入图像上滑动卷积核,对每个位置进行卷积运算,并将结果存储到输出图像中。具体来说,每一次卷积操作的计算方式如下:
- 将卷积核的每个元素与输入图像中对应的元素相乘
- 将所得到的乘积相加,得到卷积核在当前位置的输出值
- 将卷积核向右或向下移动一个位置,重复上述步骤,直到卷积核覆盖完整个输入图像。
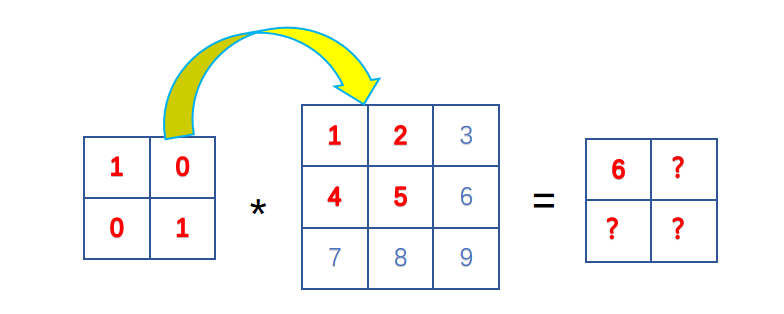
拿上面那个例子来说
- 对于输出图像中的第一个位置,卷积核与输入图像的左上角区域进行卷积运算,计算方式如下:
1 | 1*1 + 0*2 + 0*4 + 1*5 = 6 |
因此输出图像中的第一个位置的值为6。
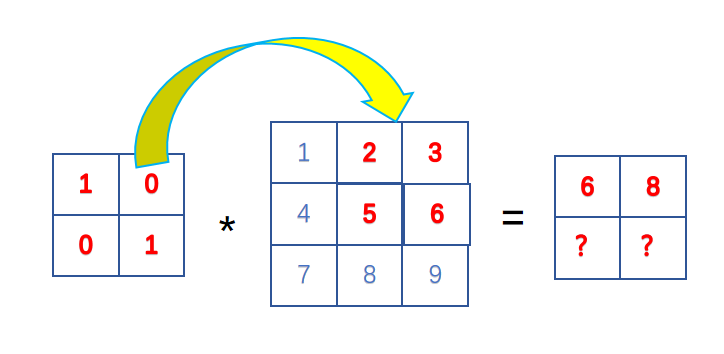
- 对于输出图像中的第二个位置,卷积核向右移动一个位置,与输入图像的右上角区域进行卷积运算,计算方式如下:
1 | 1*2 + 0*3 + 0*5 + 1*6= 8 |
因此输出图像中的第二个位置的值为6。
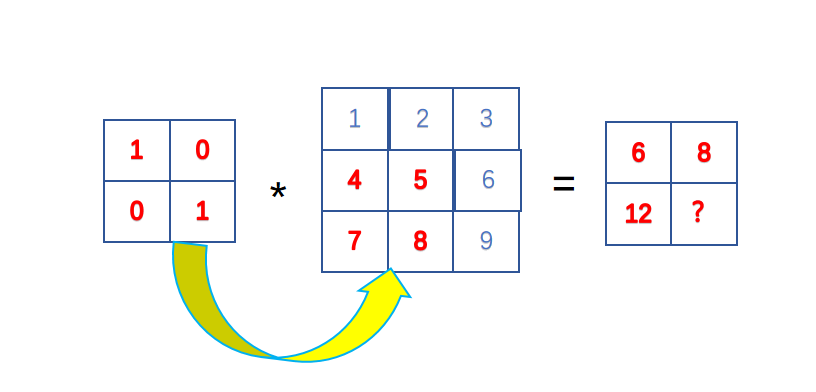
- 对于输出图像中的第三个位置,卷积核向右移动一个位置,与输入图像的左下角区域进行卷积运算,计算方式如下:
1 | 1*4 + 0*5 + 0*7 + 1*8 = 12 |
因此输出图像中的第三个位置的值为12
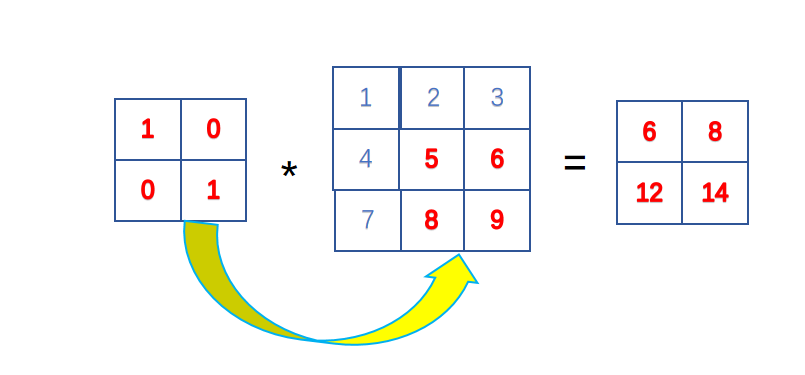
- 对于输出图像中的第四个位置,卷积核向右移动一个位置,与输入图像的右下角区域进行卷积运算,计算方式如下:
1 | 1*5 + 0*6 + 0*8 + 1*9 = 14 |
因此输出图像中的第四个位置的值为14。
上面举的例子中
卷积核大小 宽度和高度分别2,2
卷积核从左到右,从上到下遍历 将输入的图像(33)转换为*特征图(2*2)
这里得到的这个矩阵叫做特征图,可以理解为卷积层对于图像自动提取的特征,各种任务都是建立在特征之上的
对于给定的任意宽高的卷积核($高k_h 宽k_w $),对给定宽高的图像($高n_h 宽n_w$)进行卷积操作,输出的形状是可以确定的 卷积核大小
即
$(n_h-k_h+1)×(n_w-k_w+1)$
比如上面的例子中输出形状为
$(3-1+1)×(3-1+1) =2×2 $
2 现代卷积进阶武器操作
当下的卷积 会有很多辅助武器,让卷积的效果变得更好
2.1 边界 填充
我们知道经过卷积之后,输出形状有可能会变小
但有些时候我们希望输出特征图的形状维持不变,这时候就可以进行边界填充,填充后就可以维持不变
最常用的边界填充方法是零填充
对于给定的任意宽高的卷积核($高k_h 宽k_w $),对给定宽高的图像($高n_h 宽n_w$)进行卷积操作,左右上下各填充p 则输出形状为
$输出高=(n_h-k_h+2p)+1 $
$输出宽= (n_w-n_h+2p)+1$
比如特征图7*7
卷积核3*3
零填充 1
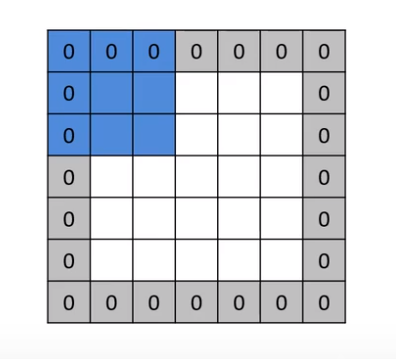
则代入输出形状代入公式
$输出高=(n_h-k_h+2p)+1 输出宽= (n_w-n_h+2p)+1$
(7-3+1+2×1) ×(7-3+1+2×1) =7×7
这也是为什么很多卷积核设计都是奇数,唯有奇数才能保证填充后前后形状不变
总结填充作用:保持输入输出的形状一致
2.2 跨步 步幅
但有些时候,我们需要降低输出特征图维度,可以指定的间隔进行卷积操作降低特征图维度,可以降低计算量。
另一方面,设置步幅可以控制特征提取的粒度。在卷积神经网络中,卷积核在输入图像上滑动时,会对输入图像的每个局部区域进行特征提取。而设置步幅可以控制卷积核在输入图像上移动的步长大小,从而控制特征提取的粒度。当步幅较小时,卷积核在输入图像上移动的步长较小,可以提取更为精细的特征信息;当步幅较大时,卷积核在输入图像上移动的步长较大,可以提取更为宏观的特征信息。
之前我们默认都是1步操作
对于给定的任意宽高的卷积核($高k_h 宽k_w $),对给定宽高的图像($高n_h 宽n_w$)进行卷积操作,左右上下各填充p 跨步S
$输出高=(n_h-k_h+2p)/S+1 $
$输出宽= (n_w-n_h+2p)/S+1$
2.3 多输入输出通道
多输入通道
在第一节的讲解中,我们默认我们的输入输出都是平面的, 只考虑了宽高的变化
但实际上,真实中往往有多层,专业术语叫做多个通道
比如图片输入往往是3通道的R,G,B 这时候我们就需要构造一个和输入相同通道的卷积核(这个例子中是3)
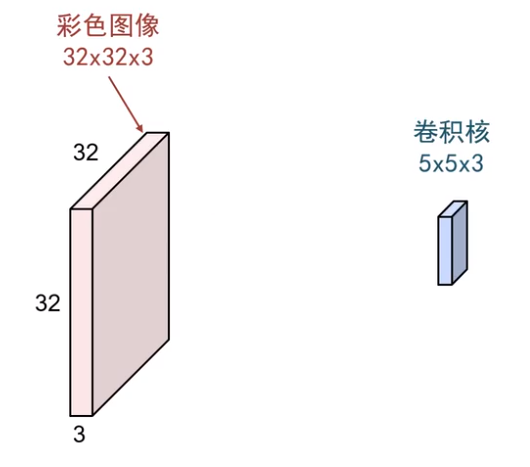
我们需要把 这样一个多通道的卷积核对齐到图像的某个位置,计算对应元素加权求和再累加,一般还会加一个偏移量
虽然卷积核是多通道的,但在一个位置加权求和累加之和只能得到一个值,意味着只能得到一层的输出
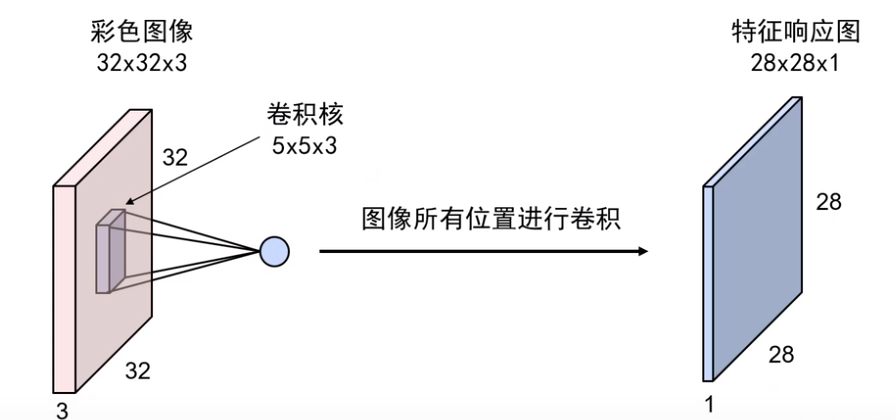
图片借鉴北京邮电大学鲁鹏老师的课程
多输出通道
如果我们想要输出变成多个,那么我们就可以使用多个卷积核
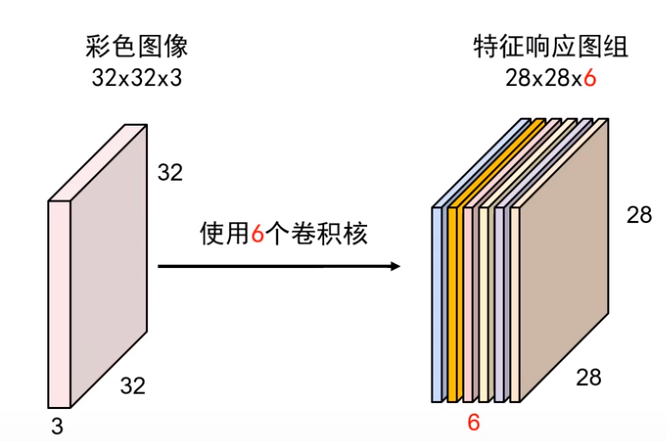
使用多少个卷积核,就会得到多少组中间特征图
图示例子是6个
2.4 汇聚 池化
除了跨步可以降低特征图大小,池化也可以
对每一个特征图独立进行,降低特征相应图组中的每个特征相应图的宽度和高度
(1)减少后续卷积层的参数数量,控制过拟合
(2)降低计算资源耗费
池化也有卷积操作一样的填充,步幅,多输入输出通道的概念,输出形状通道数计算公式和卷积都一样
比如,特征图大小4*4
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
现在我们对这个输入特征图进行2×2的最大池化操作,步幅为2,即每个子区域的大小为2×2,卷积核从左上角开始移动,每次向右移动2个像素,最后得到输出特征图大小为2×2,如下所示:
两个基本操作
最大池化
取每个子区域中最大的特征值作为该区域的输出
本例中 输出
1 | 6 8 |
平均池化
取每个子区域中所有元素的平均值作为该区域的输出
本例中输出
1 | 3.5 5.5 |
3. 卷积层设计
每一层的卷积核的
卷积核个数
卷积核尺寸大小
卷积核移动的步幅
是否进行填充
什么时候汇聚池化


